Part 1 of n: An Introduction
A bunch of my recent posts have mentioned networks. Elijah Meeks not-so-subtly hinted that it might be a good idea to discuss some of the basics of networks on this blog, and I’m happy to oblige. He already introduced network visualizations on his own blog, and did a fantastic job of it, so I’m going to try to stick to more of the conceptual issues here, gearing the discussion generally toward people with little-to-no background in networks or math, and specifically to digital humanists interested in applying network analysis to their own work. This will be part of an ongoing series, so if you have any requests, please feel free to mention them in the comments below (I’ve already been asked to discuss how social networks apply to fictional worlds, which is probably next on the list).
Some Warnings
A network is a fantastic tool in the digital humanist’s toolbox – one of many – and it’s no exaggeration to say pretty much any data can be studied via network analysis. With enough stretching and molding, you too could have a network analysis problem! As with many other science-derived methodologies, it’s fairly easy to extend the metaphor of network analysis into any number of domains.
The danger here is two-fold.
- When you’re given your first hammer, everything looks like a nail. Networks can be used on any project. Networks should be used on far fewer. Networks in the humanities are experiencing quite the awakening, and this is due in part to until-recently untapped resources. There is a lot of low-hanging fruit out there on the networks+humanities tree, and they ought to be plucked by those brave and willing enough to do so. However, that does not give us an excuse to apply networks to everything. This series will talk a little bit about when hammers are useful, and when you really should be reaching for a screwdriver.
- Methodology appropriation is dangerous. Even when the people designing a methodology for some specific purpose get it right – and they rarely do – there is often a score of theoretical and philosophical caveats that get lost when the methodology gets translated. In the more frequent case, when those caveats are not known to begin with, “borrowing” the methodology becomes even more dangerous. Ted Underwood blogs a great example of why literary historians ought to skip a major step in Latent Semantic Analysis, because the purpose of the literary historian is so very different from that of computer scientists who designed the algorithm. This series will attempt to point out some of the theoretical baggage and necessary assumptions of the various network methods it covers.
The Basics
Nothing worth discovering has ever been found in safe waters. Or rather, everything worth discovering in safe waters has already been discovered, so it’s time to shove off into the dangerous waters of methodology appropriation, cognizant of the warnings but not crippled by them.
Anyone with a lot of time and a vicious interest in networks should stop reading right now, and instead pick up copies of Networks, Crowds, and Markets (Easley & Kleinberg, 2010) and Networks: An Introduction (Newman, 2010). The first is a non-mathy introduction to most of the concepts of network analysis, and the second is a more in depth (and formula-laden) exploration of those concepts. They’re phenomenal, essential, and worth every penny.
Those of you with slightly less time, but somehow enough to read my rambling blog (there are apparently a few of you out there), so good of you to join me. We’ll start with the really basic basics, but stay with me, because by part n of this series, we’ll be going over the really cool stuff only ninjas, Gandhi, and The Rolling Stones have worked on.
Networks
The word “network” originally meant just that: “a net-like arrangement of threads, wires, etc.” It later came to stand for any complex, interlocking system. Stuff and relationships.
Generally, network studies are made under the assumption that neither the stuff nor the relationships are the whole story on their own. If you’re studying something with networks, odds are you’re doing so because you think the objects of your study are interdependent rather than independent. Representing information as a network implicitly suggests not only that connections matter, but that they are required to understand whatever’s going on.
Oh, I should mention that people often use the word “graph” when talking about networks. It’s basically the mathy term for a network, and its definition is a bit more formalized and concrete. Think dots connected with lines.
Because networks are studied by lots of different groups, there are lots of different words for pretty much the same concepts. I’ll explain some of them below.
The Stuff
Stuff (presumably) exists. Eggplants, true love, the Mary Celeste, tall people, and Terry Pratchett’s Thief of Time all fall in that category. Network analysis generally deals with one or a small handful of types of stuff, and then a multitude of examples of that type.
Say the type we’re dealing with is a book. While scholars might argue the exact lines of demarcation separating book from non-book, I think we can all agree that most of the stuff in my bookshelf are, in fact, books. They’re the stuff. There are different examples of books; a quotation dictionary, a Poe collection, and so forth.
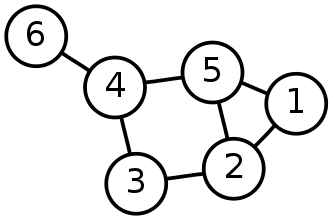
I’ll call this assortment of stuff nodes. You’ll also hear them called vertices (mostly from the mathematicians and computer scientists), actors (from the sociologists), agents (from the modelers), or points (not really sure where this one comes from).
The type of stuff corresponds to the type of node. The individual examples are the nodes themselves. All of the nodes are books, and each book is a different node.
Nodes can have attributes. Each node, for example, may include the title, the number of pages, and the year of publication.
A list of nodes could look like this:
| Title | # of pages | year of publication | | ----------------------------------------------------------- | | Graphs, Maps, and Trees | 119 | 2005 | | How The Other Half Lives | 233 | 1890 | | Modern Epic | 272 | 1995 | | Mythology | 352 | 1942 | | Macroanalysis | unknown | 2011 |
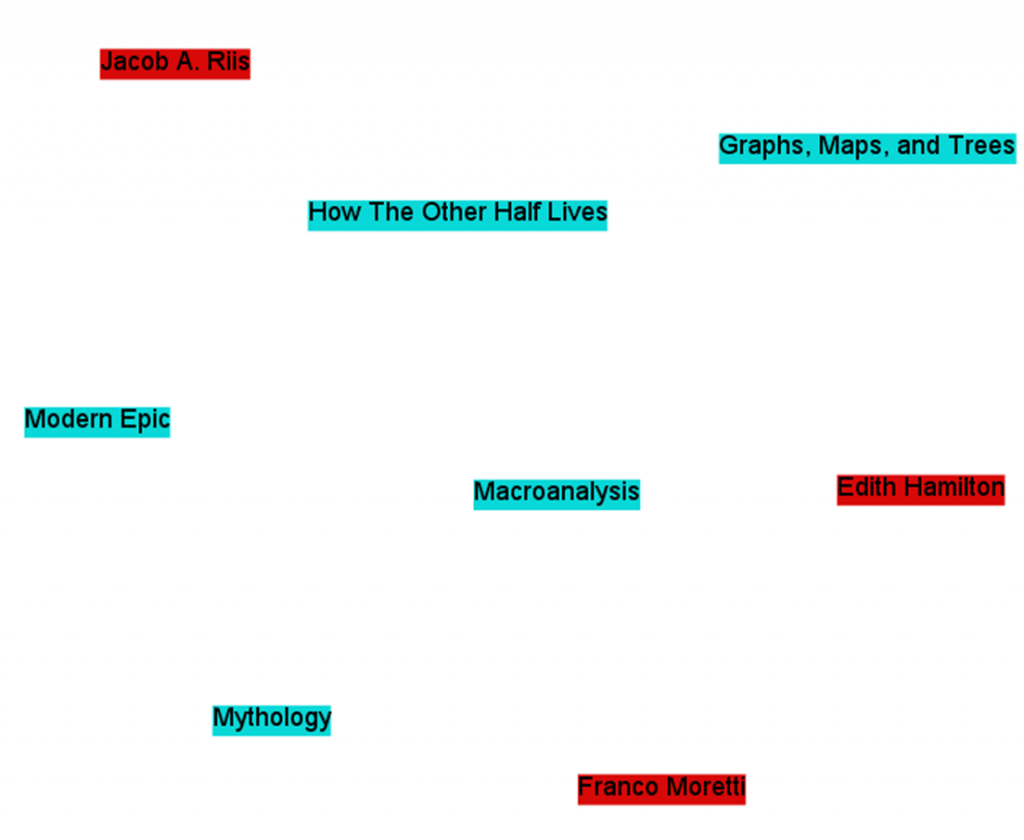
We can get a bit more complicated and add more node types to the network. Authors, for example. Now we’ve got a network with books and authors (but nothing linking them, yet!). Franco Moretti and Graphs, Maps, and Trees are both nodes, although they are of different varieties, and not yet connected. We would have a second list of nodes, part of the same network, that might look like this:
| Author | Birth | Death | | --------------------------------- | | Franco Moretti | ? | n/a | | Jacob A. Riis | 1849 | 1914 | | Edith Hamilton | 1867 | 1963 | | Matthew Jockers | ? | n/a |
A network with two types of nodes is called 2-mode, bimodal, or bipartite. We can add more, making it multimodal. Publishers, topics, you-name-it. We can even add seemingly unrelated node-types, like academic conferences, or colors of the rainbow. The list goes on. We would have a new list for each new variety of node.
Presumably we could continue adding nodes and node-types until we run out of stuff in the universe. This would be a bad idea, and not just because it would take more time, energy, and hard-drives than could ever possibly exist.
As it stands now, network science is ill-equipped to deal with multimodal networks. 2-mode networks are difficult enough to work with, but once you get to three or more varieties of nodes, most algorithms used in network analysis simply do not work. It’s not that they can’t work; it’s just that most algorithms were only created to deal with networks with one variety of node.
This is a trap I see many newcomers to network science falling into, especially in the Digital Humanities. They find themselves with a network dataset of, for example, authors and publishers. Each author is connected with one or several publishers (we’ll get into the connections themselves in the next section), and the up-and-coming network scientist loads the network into their favorite software and visualizes it. Woah! A network!
Then, because the software is easy to use, and has a lot of buttons with words that from a non-technical standpoint seem to make a lot of sense, they press those buttons to see what comes out. Then, they change the visual characteristics of the network based on the buttons they’ve pressed.
Let’s take a concrete example. Popular network software Gephi comes with a button that measures the centrality of nodes. Centrality is a pretty complicated concept that I’ll get into more detail later, but for now it’s enough to say that it does exactly what it sounds like; it finds how central, or important, each node is in a network. The newcomer to network analysis loads the author-publisher network into Gephi, finds the centrality of every node, and then makes the nodes bigger that have the highest centrality.
The issue here is that, although the network loads into Gephi perfectly fine, and although the centrality algorithm runs smoothly, the resulting numbers do not mean what they usually mean. Centrality, as it exists in Gephi, was fine-tuned to be used with single mode networks, whereas the author-publisher network is bimodal. Centrality measures have been made for bimodal networks, but those algorithms are not included with Gephi.
Most computer scientists working with networks do so with only one or a few types of nodes. Humanities scholars, on the other hand, are often dealing with the interactions of many types of things, and so the algorithms developed for traditional network studies are insufficient for the networks we often have. There are ways of fitting their algorithms to our networks, or vice-versa, but that requires fairly robust technical knowledge of the task at hand.
Besides dealing with the single mode / multimodal issue, humanists also must struggle with fitting square pegs in round holes. Humanistic data are almost by definition uncertain, open to interpretation, flexible, and not easily definable. Node types are concrete; your object either is or is not a book. Every book-type thing shares certain unchanging characteristics.
This reduction of data comes at a price, one that some argue traditionally divided the humanities and social sciences. If humanists care more about the differences than the regularities, more about what makes an object unique rather than what makes it similar, that is the very information they are likely to lose by defining their objects as nodes.
This is not to say it cannot be done, or even that it has not! People are clever, and network science is more flexible than some give it credit for. The important thing is either to be aware of what you are losing when you reduce your objects to one or a few types of nodes, or to change the methods of network science to fit your more complex data.
The Relationships
Relationships (presumably) exist. Friendships, similarities, web links, authorships, and wires all fall into this category. Network analysis generally deals with one or a small handful of types of relationships, and then a multitude of examples of that type.
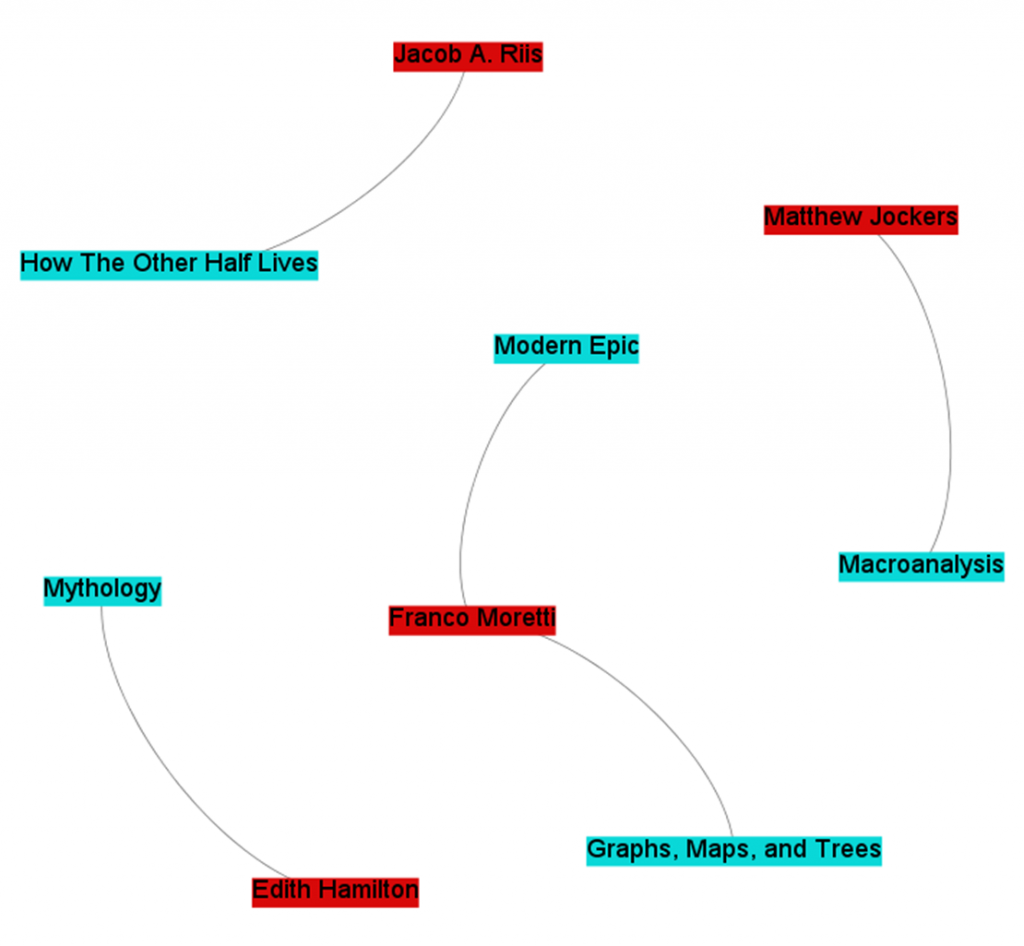
Say the type we’re dealing with is an authorship. Books (the stuff) and authors (another kind of stuff) are connected to one-another via the authorship relationship, which is formalized in the phrase “X is an author of Y.” The individual relationships themselves are of the form “Franco Moretti is an author of Graphs, Maps, and Trees.”
Much like the stuff (nodes), relationships enjoy a multitude of names. I’ll call them edges. You’ll also hear them called arcs, links, ties, and relations. For simplicity sake, although edges are often used to describe only one variety of relationship, I’ll use it for pretty much everything and just add qualifiers when discussing specific types. The type of relationship corresponds to the type of edge. The individual examples are the edges themselves.
Individual edges are defined, in part, by the nodes that they connect.
A list of edges could look like this:
| Person | Is an author of | | ----------------------------------------------------- | | Franco Moretti | Modern Epic | | Franco Moretti | Graphs, Maps, and Trees | | Jacob A. Riis | How The Other Half Lives | | Edith Hamilton | Mythology | | Matthew Jockers | Macroanalysis |
Notice how, in this scheme, edges can only link two different types of nodes. That is, a person can be an author of a book, but a book cannot be an author of a book, nor can a person an author of a person. For a network to be truly bimodal, it must be of this form. Edges can go between types, but not among them.
This constraint may seem artificial, and in some sense it is, but for reasons I’ll get into in a later post, it is a constraint required by most algorithms that deal with bimodal networks. As mentioned above, algorithms are developed for specific purposes. Single mode networks are the ones with the most research done on them, but bimodal networks certainly come in a close second. They are networks with two types of nodes, and edges only going between those types.
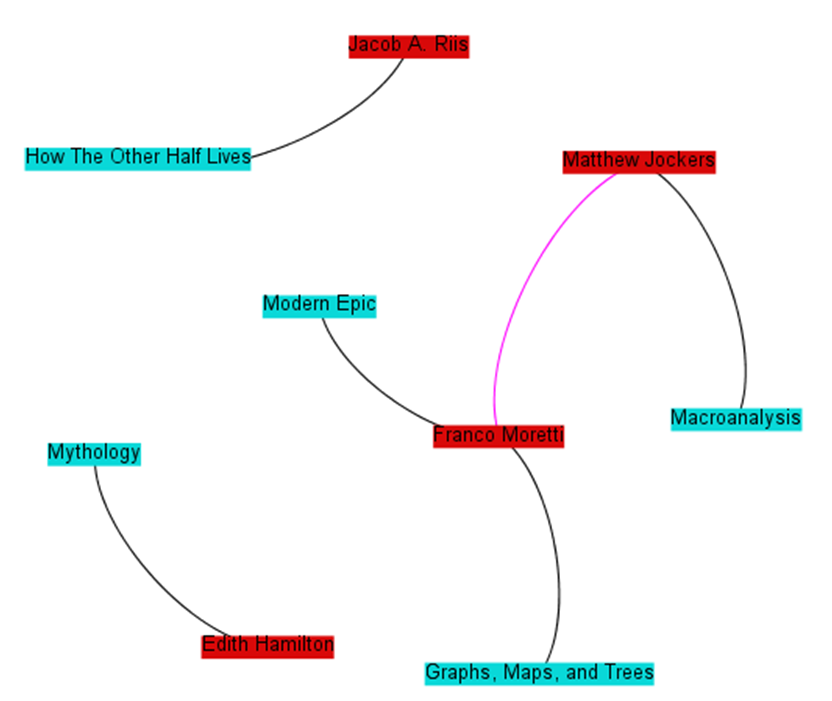
Of course, the world humanists care to model is often a good deal more complicated than that, and not only does it have multiple varieties of nodes – it also has multiple varieties of edges. Perhaps, in addition to “X is an author of Y” type relationships, we also want to include “A collaborates with B” type relationships. Because edges, like nodes, can have attributes, an edge list combining both might look like this.
| Node1 | Node 2 | Edge Type | | ----------------------------------------------------- | ----------------- | | Franco Moretti | Modern Epic | is an author of | | Franco Moretti | Graphs, Maps, and Trees | is an author of | | Jacob A. Riis | How The Other Half Lives | is an author of | | Edith Hamilton | Mythology | is an author of | | Matthew Jockers | Macroanalysis | is an author of | | Matthew Jockers | Franco Moretti | collaborates with |
Notice that there are now two types of edges: “is an author of” and “collaborates with.” Not only are they two different types of edges; they act in two fundamentally different ways. “X is an author of Y” is an asymmetric relationship; that is, you cannot switch out Node1 for Node2. You cannot say “Modern Epic is an author of Franco Moretti.” We call this type of relationship a directed edge, and we generally represent that visually using an arrow going from one node to another.
“A collaborates with B,” on the other hand, is a symmetric relationship. We can switch out “Matthew Jockers collaborates with Franco Moretti” with “Franco Moretti collaborates with Matthew Jockers,” and the information represented would be exactly the same. This is called an undirected edge, and is usually represented visually by a simple line connecting two nodes.
Most network algorithms and visualizations break down when combining these two flavors of edges. Some algorithms were designed for directed edges, like Google’s PageRank, whereas other algorithms are designed for undirected edges, like many centrality measures. Combining both types is rarely a good idea. Some algorithms will still run when the two are combined, however the results usually make little sense.
Both directed and undirected edges can also be weighted. For example, I can try to make a network of books, with those books that are similar to one another sharing an edge between them. The more similar they are, the heavier the weight of that edge. I can say that every book is similar to every other on a scale from 1 to 100, and compare them by whether they use the same words. Two dictionaries would probably connect to one another with an edge weight of 95 or so, whereas Graphs, Maps, and Trees would probably share an edge of weight 5 with How The Other Half Lives. This is often visually represented by the thickness of the line connecting two nodes, although sometimes it is represented as color or length.
It’s also worth pointing out the difference between explicit and inferred edges. If we’re talking about computers connected on a network via wires, the edges connecting each computer actually exist. We can weight them by wire length, and that length, too, actually exists. Similarly, citation linkages, neighbor relationships, and phone calls are explicit edges.
We can begin to move into interpretation when we begin creating edges between books based on similarity (even when using something like word comparisons). The edges are a layer of interpretation not intrinsic in the objects themselves. The humanist might argue that all edges are intrinsic all the way down, or inferred all the way up, but in either case there is a difference in kind between two computers connected via wires, and two books connected because we feel they share similar topics.
As such, algorithms made to work on one may not work on the other; or perhaps they may, but their interpretative framework must change drastically. A very central computer might be one in which, if removed, the computers will no longer be able to interact with one another; a very central book may be something else entirely.
As with nodes, edges come with many theoretical shortcomings for the humanist. Really, everything is probably related to everything else in its light cone. If we’ve managed to make everything in the world a node, realistically we’d also have some sort of edge between pretty much everything, with a lesser or greater weight. A network of nodes where almost everything is connected to almost everything else is called dense, and dense networks networks are rarely useful. Most network algorithms (especially ones that detect communities of nodes) work better and faster when the network is sparse, when most nodes are only connected to a small percentage of other nodes.
To make our network sparse, we often must artificially cut off which edges to use, especially with humanistic and inferred data. That’s what Shawn Graham showed us how to do when combining topic models with networks. The network was one of authors and topics; which authors wrote about which topics? The data itself connected every author to every topic to a greater or lesser degree, but such a dense network would not be very useful, so Shawn limited the edges to the highest weighted connections between an author and a topic. The resulting network looked like this, when it otherwise would have looked like a big ball of spaghetti and meatballs.
Unfortunately, given that humanistic data are often uncertain and biased to begin with, every arbitrary act of data-cutting has the potential to add further uncertainty and bias to a point where the network no longer provides meaningful results. The ability to cut away just enough data to make the network manageable, but not enough to lose information, is as much an art as it is a science.
Hypergraphs & Multigraphs
Mathematicians and computer scientists have actually formalized more complex varieties of networks, and they call them hypergraphs and multigraphs. Because humanities data are often so rich and complex, it may be more appropriate to represent it using these representations. Unfortunately, although ample research has been done on both, most out-of-the-box tools support neither. We have to build them for ourselves.
A hypergraph is one in which more than two nodes can be connected by one edge. A simple example would be a “is a sibling of” relationship, where the edge connected three sisters rather than two. This is a symmetric, undirected edge, but perhaps there can be directed edges as well, of the type “Alex convinced Betty to run away from Carl.”
A multigraph is one in which multiple edges can connect any two nodes. We can have, for example, a transportation graph between cities. A edge exists for every transportation route. Realistically, many routes can exist between any two cities; some by plane, several different highways, trains, etc.
I imagine both of these representations will be important for humanists going forward, but rather than relying on that computer scientist who keeps hanging out in the history department, we ourselves will have to develop algorithms that accurately capture exactly what it is we are looking for. We have a different set of problems, and though the solutions may be similar, they must be adapted to our needs.
Side note: RDF Triples
Digital humanities loves RDF. RDF basically works using something called a triple; a subject, a predicate, and an object. “Moretti is an author of Graphs, Maps, and Trees” is an example of a triple, where “Moretti” is the subject, “is an author of” is the predicate, and “Graphs, Maps, and Trees” is the object. As such, nearly all RDF documents can be represented as a directed network. Whether that representation would actually be useful depends on the situation.
Side note: Perspectives
Context is key, especially in the humanities. One thing the last few decades has taught us is that perspectives are essential, and any model of humanity that does not take into account its multifaceted nature is doomed to be forever incomplete. According to Alex, Betty and Carl are best friends. According to Carl, he can’t actually stand Betty. The structure and nature of a network might change depending on the perspective of a particular node, and I know of no model that captures this complexity. If you’re familiar with something that might capture this, or are working on it yourself, please let me know via comments or e-mail.
Networks, Revisited
The above post discussed the simplest units of networks; the stuff and the relationships that connect them. Any network analysis approach must subscribe to and live with that duality of objects. Humanists face problems from the outset; data that does not fit neatly into one category or the other, complex situations that ought not be reduced, and methods that were developed with different purposes in mind. However, network analysis remains a viable methodology for answering and raising humanistic questions – we simply must be cautious, and must be willing to get our hands dirty editing the algorithms to suit our needs.
In the coming posts of this series, I’ll discuss various introductory topics including data representations, basic metrics like degree, centrality, density, clustering, and path length, as well as ways to link old network analysis concepts with common humanist problems. I’ll also try to highlight examples from the humanities, and raise methodological issues that come with our appropriation of somebody else’s algorithms.
This will probably be the longest of the posts, as some concepts are fairly central and must be discussed all-at-once. Again, if anybody has any particular concepts of network analysis they’d like to see discussed, please don’t hesitate to comment with your request.

If one wanted to do multimodal analysis, is there a way to do basic or bimodal analysis on several sets of data and then overlay them or correlate them? I’m thinking of looking at various relationships obtaining amongst members of a professional society, their home institutions, their topics, etc. Would it be possible to graph the names, then the institutions, then the topics, etc. and then find some way to correlate that data to produce a complex representation of the centrality of persons, places, topics, etc?
Thanks for the post, by the way — very, very helpful.
That’s a question I’ve struggled with before, as well. While it is conceivable to make a network that combines all of those elements, and with some finagling perhaps an algorithm that will encode meaningful information about all elements, I’m not really convinced that’s the best way to go.
Whether you’re looking for a visual or numerical representation, only one representation is rarely enough. For visualizations, although getting everything distilled down into one picture is satisfying and great PR for your project, it constrains you to two (at most three) axes, and then a few extra dimensions for color, size, etc. Sometimes that’s sufficient; for example, in the above question, you can find centrality of people, institutions, and topics by themselves, then connect them all in one large graph, sized by centrality, and colored by what “type” of node each is. If your data are too large, however, this graph will become unreadable pretty fast. The better option might be to represent each node type individually in a separate representation, and only then perhaps all of them together for a broader view of how they all connect.
For simple numerical scores, one representation is even worse. Scores are inherently ordinal, so you’ll get a list of nodes where some topic is more central than some person, who is himself more central than some institution. It would be hard finding meaning in those orders, so it again might be best to stick with multiple representations.
In either case, don’t sacrifice understandability for the desire to squeeze everything into one picture.
That being said, you can also find edges between every person through professional society affiliation, institution, topic, etc., and make each of those associations different edge types, with each edge weighted. Some software packages allow visualizing multiple edges between nodes, so you view, say, four different edges between Alice and Bob. Or, you can add them all together in some way and visualize the network that way, but you’ll be losing the individual types of connections in the process.
Hey Scott,
This is a really helpful, clear, post on what networks do and don’t do well. One thing that you might consider clarifying is what you mean by “useful,” as when you say that “dense networks networks are rarely useful.” I gather that by “useful” you mean “susceptible to algorithmic analysis.” But of course there are plenty of other things for which networks are useful.
d
Dan, thanks for the comment, that’s a great point, I’ll update accordingly in my next write-through.
Hi Scott, thanks for this very clear and to-the-point post. When I recently experimented with making a network of crime fiction novels and their topics, I had to deal precisely with some of the issues you discuss: how to deal with a bimodal network and how to deal with high density.
As for the bimodality, for example, depending on the relative number of topics and novels, topics may just on account of their smaller number have higher centrality, which I guess would then be a misleading measure. In my case, even with a ratio of 200 novels to 40 topics, this is certainly noticeable.
And as for the sparsity issue, cutting out a relatively large part of the low-scoring novel-topic associations certainly helped with visualization. But it seems choosing the cut-off point is a matter of trial-and-error and experience. In my case, I took out any novel-topic associations with a score lower than 0.05, of which there were many, reducing the number of edges by about two thirds. But this will vary with the number of documents and number of topics in the dataset.
Anyway, this post is still a good read!